Toán 10 tập 2 trang 73: Bài tập cuối chương 9

Giải toán 10 tập 2 trang 73 bài tập cuối chương 9 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán 10 tập 2 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 10 tập 2 trang 73

Bài 1 trang 73 Toán 10 tập 2

Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a. Chứng minh ABCD là hình vuông.

b. Tìm tọa độ tâm I của hình vuông ABCD.

Hướng dẫn:

a. Ta có: $\vec{AB} = (-1; 3), \vec{DC} = (-1; 3)$ => $\vec{AB} = \vec{DC}$

=> ABCD là hình bình hành.

Lại có: $\vec{AD}$ = (3; 1) => $\vec{AB}. \vec{AD}$ = -1. 3 + 3. 1 = 0

=> $\vec{AB} \perp \vec{AD}$ hay $AB \perp AD$

=> Hình bình hành ABCD là hình chữ nhật.

Ta có: AD = $|\vec{AD}| = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$

AB = $|\vec{AB}| = \sqrt{(-1)^{2} + 3^{2}} = \sqrt{10}$

• AB = AD => Hình chữ nhật ABCD là hình vuông .

b. Tâm I của hình vuông ABCD là trung điểm của AC => I = $(\frac{2 + 4}{2}; \frac{1+5}{2})$ => I = (3; 3)

Vậy I = (3; 3).

Bài 2 trang 73 Toán 10 tập 2

Cho AB và CD là dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.

Hướng dẫn:

Chọn hệ tọa độ Oxy như hình vẽ. A(a; 0), B(b; 0), C(0; c), D(0; d). Hai dây cung AB và CD vuông góc với nhau tại E (trùng với gốc tọa độ O).

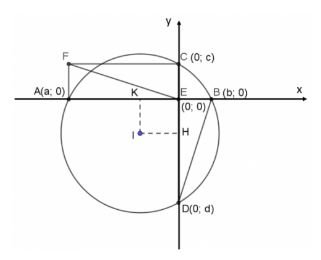
Vì ACEF là hình chữ nhật nên F(a; c).

Gọi I là tâm đường tròn (O), K và H lần lượt là chân đường cao hạ từ I tới AB, CD.

=> K là trung điểm của AB => K = $(\frac{a + b}{2}; 0)$

H là trung điểm của CD => H = $(0; \frac{c + d}{2})$

=> I = $(\frac{a + b}{2}; \frac{c + d}{2})$

Ta có: $\vec{IA} = (a – \frac{a + b}{2}; -\frac{c + d}{2}) = (\frac{a – b}{2}; -\frac{c + d}{2})$

$\vec{IC} = ( -\frac{a + b}{2}; c – \frac{c + d}{2}) = (-\frac{a + b}{2}; \frac{c – d}{2})$

Vì IA = IC (=R) => $(\frac{a – b}{2})^{2} + (-\frac{c + d}{2})^{2} = (-\frac{a + b}{2})^{2} + (\frac{c – d}{2})^{2}$

• $ (a – b)^{2} + (c + d)^{2} = (a + b)^{2} + (c – d)^{2}$

<=> $a^{2} – 2ab + b^{2} + c^{2} + 2cd + d^{2} = a^{2} + 2ab + b^{2} + c^{2} – 2cd + d^{2}$

<=> $4ab = 4cd \Leftrightarrow ab = cd \Leftrightarrow ab – cd = 0$

<=> $\vec{EF}. \vec{BD} = (-a).(-b) – c.d = ab – cd = 0$

=> $\vec{EF} \perp \vec{BD}$ hay $EF \perp BD$

Bài 3 trang 73 Toán 10 tập 2

Tìm tọa độ giao điểm và góc giữa hai đường thẳng $d_{1}$ và $d_{2}$ trong mỗi trường hợp sau:

a.$d_{1}$: x – y + 2 = 0 và $d_{2}$: x + y + 4 = 0;

b. $d_{1}: \left\{\begin{matrix}x = 1 + t\\y = 3 + 2t \end{matrix}\right.$ và $d_{2}$: x – 3y + 2 = 0;

c. $d_{1}: \left\{\begin{matrix}x = 2 – t\\y = 5 + 3t \end{matrix}\right.$ và $d_{2}$:$\begin{cases}x&=1+3t’\\y&=3+t’\end{cases}$

Hướng dẫn:

a. Đường thẳng $d_{1}$ và $d_{2}$

có vectơ pháp tuyến lần lượt là $\vec{n_{1}}$ = (1; -1) và $\vec{n_{2}}$ = (1; 1).

Ta có:$\vec{n_{1}}. \vec{n_{2}}$ = 1. 1 + (-1). 1 = 0 nên $\vec{n_{1}}$ và $\vec{n_{2}}$

là hai vectơ vuông góc => $d_{1} \perp d_{2}$ => $(d_{1}, d_{2}) = 90^{\circ}$.

Giao điểm M của $d_{1}$ và $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}x – y + 2 = 0\\x + y + 4 = 0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = -3 \\y = -1\end{matrix}\right.$

Vậy $d_{1}$ và $d_{2}$ vuông góc và cắt nhau tại M(-3; -1).

b. Ta có: $\vec{u_{1}}$ = (1; 2) là vectơ chỉ phương của $d_{1}$ => $\vec{n_{1}}$ = (2; -1)

là vectơ pháp tuyến của $d_{1}$.

Phương trình tổng quát của d₁ đi qua điểm A(1; 3) và nhận$\vec{n_{1}}$ = (2; -1) làm vectơ pháp tuyến là: 2(x – 1) – (y – 3) = 0 => 2x – y + 1 = 0

Đường thẳng $d_{2}$ có vectơ pháp tuyến là $\vec{n_{2}}$ = (1; -3)

Ta có: $\frac{2}{1} \neq \frac{-1}{-3}$ => $\vec{n_{1}}$ và $\vec{n_{2}}$ là hai vectơ không cùng phương.

=> $d_{1}$ và $d_{2}$ cắt nhau. Giao điểm M của $d_{1}$ và $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}2x – y + 1 = 0\\x – 3y + 2 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{-1}{5}\\y = \frac{3}{5}\end{matrix}\right.$

Ta có: $cos(d_{1}, d_{2}) = \frac{|2. 1 + (-1). (-3)|}{\sqrt{2^{2} + (-1)^{2}}.\sqrt{1^{2} + (-3)^{2}}} = \frac{\sqrt{2}}{2} \Rightarrow (d_{1}, d_{2}) = 45^{\circ}$

Vậy $d_{1}$ cắt $d_{2}$ tại điểm $M(\frac{-1}{5}; \frac{3}{5})$ và $(d_{1}, d_{2}) = 45^{\circ}.$

c. Phương trình tổng quát của $d_{1}$ và $d_{2}$ lần lượt là:

$d_{1}$: 3x + y – 11 = 0 và $d_{2}$: x – 3y + 8 = 0

Ta có: $\vec{n_{1}}. \vec{n_{2}} = 3. 1 + 1. (-3) = 0 \Rightarrow \vec{n_{1}} \perp \vec{n_{2}} hay d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}$.

Giao điểm M của đường thẳng $d_{1}$ và $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}3x + y – 11 = 0\\x – 3y + 8 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{5}{2}\\y = \frac{7}{2}\end{matrix}\right.$

Vậy $d_{1}$ và $d_{2}$ vuông góc và cắt nhau tại $M(\frac{5}{2}; \frac{7}{2})$.

Bài 4 trang 73 Toán 10 tập 2

Tính bán kính của đường tròn tâm M(-2; 3) và tiếp xúc với đường thẳng:

Hướng dẫn:

d: 14x – 5y + 60 = 0

Ta có: R = d(M; d) = $\frac{|14. (-2) – 5. 3 + 60|}{\sqrt{14^{2} + (-5)^{2}}} = \frac{\sqrt{221}}{13}$

Bài 5 trang 73 Toán 10 tập 2

Tính khoảng cách giữa hai đường thẳng: $\Delta’$: 3x+4y-27=0

Hướng dẫn:

Ta có: $\frac{6}{3} = \frac{8}{4} \neq \frac{-13}{-27} \Rightarrow \Delta // \Delta’$

Lấy điểm $A(0; \frac{13}{8}) \in \Delta$.

Ta có: $d(\Delta, \Delta’)$

Bài 6 trang 73 Toán 10 tập 2

Tìm tâm và bán kính của các đường tròn có phương trình:

a. $(x – 2)^{2} + (y – 7)^{2}$ = 64;

b. $(x + 3)^{2} + (y + 2)^{2}$ = 8;

c. $x^{2} + y^{2} – 4x – 6y – 12$ = 0.

Hướng dẫn:

a. Phương trình đường tròn có dạng $(x – a)^{2} + (y – b)^{2} = R^{2}$

=> Đường tròn có tâm I(2; 7) và bán kính R = 8.

b. Phương trình đường tròn có dạng $(x – a)^{2} + (y – b)^{2} = R^{2}$

=> Đường tròn có tâm I(-3; -2) và bán kính R = $2\sqrt{2}$.

c. Phương trình có dạng $x^{2} + y^{2} – 2ax – 2by + c = 0$ với a = 2, b = 3, c = -12

Ta có: $a^{2} + b^{2} – c = 2^{2} + 3^{2} + 12 = 25$

Vậy đường tròn có tâm I(2; 3) và bán kính R = $\sqrt{25}$ = 5.

Bài 7 trang 73 Toán 10 tập 2

Lập phương trình đường tròn trong các trường hợp sau:

a. Có tâm I(-2; 4) và bán kính bằng 9;

b. Có tâm I(1; 2) và đi qua điểm A(4; 5);

c. Đi qua hai điểm A(4; 1), B(6; 5) và có tâm nằm trên đường thẳng 4x + y -16 = 0;

d. Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là a, tung độ là b.

Hướng dẫn:

a. Phương trình đường tròn có tâm I(-2; 4) và bán kính R = 4 là:

$(x + 2)^{2} + (y – 4)^{2}$ = 16

b. Ta có $R = IA = \sqrt{(4 – 1)^{2} + (5 – 2)^{2}} = 3\sqrt{2}$

Phương trình đường tròn có tâm I(1; 2) và bán kính R = $3\sqrt{2}$ là:

$(x – 1)^{2} + (y – 2)^{2} = 18$

c. Phương trình đường tròn tâm I(a; b) có dạng: $x^{2} + y^{2} – 2ax – 2by + c = 0$

Vì I(a; b) thuộc đường thẳng 4x + y – 16 = 0 và các điểm A(4; 1), B(6; 5) thuộc đường tròn nên ta có hệ phương trình sau:

$\left\{\begin{matrix}4a + b – 16 = 0\\4^{2} + 1^{2} – 8a-2b +c = 0\\ 6^{2} + 5^{2} – 12a – 10b + c = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}4a + b – 16 = 0\\ 8a+2b -c = 17\\ 12a + 10b – c = 61\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}a = 3\\b = 4 \\ c = 15\end{matrix}\right.$

Vậy phương trình đường tròn là: $x^{2} + y^{2} – 6x – 8y + 15 = 0$

d. Phương trình đường tròn (C) tâm I(m; n) có dạng:$x^{2} + y^{2} – 2mx – 2ny + c = 0$

Vì O(0;0) \in (C) nên thay tọa độ O(0; 0) vào (C) ta được c = 0

Vì (C) cắt trục hoành tại điểm có tọa độ (a; 0) và cắt trục tung tại điểm có tọa độ (0; b) nên ta có:

$\left\{\begin{matrix}a^{2} – 2ma = 0\\b^{2} – 2nb = 0\end{matrix}\right.$ => $\left\{\begin{matrix} m = \frac{a}{2}\\n = \frac{b}{2}\end{matrix}\right.$ $(a \neq 0, b\neq 0)$

Vậy phương trình đường tròn (C) là:$x^{2} + y^{2} – ax – by$ = 0

Bài 8 trang 73 Toán 10

Viết phương trình tiếp tuyến của đường tròn (C): $(x – 5)^{2} + (y – 3)^{2} = 100$ tại điểm M(11; 11)

Hướng dẫn:

Ta có: (C) có tâm I(5; 3).

Phương trình tiếp tuyến của đường tròn (C) tại M(11; 11) là:

(5 – 11)(x – 11) + (3 – 11)(y – 11) = 0

<=> -6x – 8y + 154 = 0

<=> 3x + 4y – 77 = 0

Bài 9 trang 73 Toán 10

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:

a. $\frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$;

b. $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$;

c. $x^{2} + 16y^{2} = 16$

Hướng dẫn:

a. (E): $\frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

\Rightarrow a = 10; b = 6 => c = $\sqrt{a^{2} – b^{2}} = \sqrt{10^{2} – 6^{2}}$ = 8

=> Tọa độ các tiêu điểm là: (-8; 0) và (8; 0)

Tọa độ các đỉnh là: (-10; 0), (10; 0), (0; -6); (0; 6)

Độ dài trục lớn bằng 2a = 2. 10 = 20; độ dài trục nhỏ bằng 2b = 2. 6 = 12.

b. (E): $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

=> a = 5; b = 4 \Rightarrow c = $\sqrt{a^{2} – b^{2}} = \sqrt{5^{2} – 4^{2}} = 3$

=> Tọa độ các tiêu điểm là: (-3; 0) và (3; 0)

Tọa độ các đỉnh là: (-5; 0), (5; 0), (0; -4); (0; 4)

Độ dài trục lớn bằng 2a = 2. 5 = 10; độ dài trục nhỏ bằng 2b = 2. 4 = 8.

c. Ta có: $x^{2} + 16y^{2} = 16 \Leftrightarrow \frac{x^{2}}{16} + y^{2} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

=> a = 4; b = 1 => c = $\sqrt{a^{2} – b^{2}} = \sqrt{4^{2} – 1^{2}} = \sqrt{15}$

=> Tọa độ các tiêu điểm là: $(-\sqrt{15}; 0)$ và $(\sqrt{15}; 0)$

Tọa độ các đỉnh là: (-4; 0), (4; 0), (0; -1); (0; 1)

Độ dài trục lớn bằng 2a = 2. 4 = 8; độ dài trục nhỏ bằng 2b = 2. 1 = 2.

Toán 10 tập 2 trang 74

Bài tập 10 trang 74 Toán lớp 10 Tập 2

Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:

a) Đỉnh (5; 0), (0; 4);

b) Đỉnh (5; 0), tiêu điểm (3; 0);

c) Độ dài trục lớn 16, độ dài trục nhỏ 12;

d) Độ dài trục lớn 20, tiêu cự 12.

Lời giải:

a) Elip có đỉnh (5; 0), (0; 4) ⇒ a = 5; b = 4.

⇒ Phương trình elip (E) là: $\frac{x^2}{25} + \frac{y^2}{16} = 1$

Vậy elip thỏa mãn điều kiện đỉnh (5; 0), (0; 4) là : $\frac{x^2}{25} + \frac{y^2}{16} = 1$

b) Elip có đỉnh (5; 0) ⇒ a = 5; tiêu điểm (3; 0) ⇒ c = 3

=> b = $\sqrt{a^2 – c^2} = \sqrt{5^2 – 3^2} = 4$

Vậy phương trình elip cần tìm là $\frac{x^2}{64} + \frac{y^2}{36} = 1$

d) Vì độ dài trục lớn 20, tiêu cự 12 nên ta có: 2a = 20; 2c = 12

⇒ a = 10; c = 6

=> $b = \sqrt{a^2 – c^2} = \sqrt{10^2 – 6^2} = 8$

⇒ Phương trình elip (E) là: $\frac{x^2}{100} + \frac{y^2}{64} = 1$

Vậy phương trình elip cần tìm là: $\frac{x^2}{100} + \frac{y^2}{64} = 1$

Bài tập 11 trang 74 Toán lớp 10 tập 2

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:

a) $\frac{x^2}{16} – \frac{y^2}{9} = 1$

b) $\frac{x^2}{64} – \frac{y^2}{36} = 1$

c) $\frac{x^2}{16} – y^2 = 1$

d) $9x^2 – 16y^2 = 144$

Lời giải:

a) Với hypebol (H): $\frac{x^2}{16} – \frac{y^2}{9} = 1$

Phương trình hypebol (H) có dạng: $\frac{x^2}{a^2} – \frac{y^2}{b^2}$ = 1

• a = 4; b= 3=> c= $\sqrt{a^2 + b^2} = \sqrt{4^2 + 3^2}$=5

Vậy tọa độ các tiêu điểm là (−5; 0), (5; 0).

Tọa độ các đỉnh là (−4; 0), (4; 0).

Độ dài trục thực là: 2a = 2. 4 = 8; độ dài trục ảo là: 2b = 2. 3 = 6.

b) Với hypebol (H):

$\frac{x^2}{64} – \frac{y^2}{36} = 1$

Phương trình hypebol (H) có dạng: $\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1$

• a=8;b=6=>c =$\sqrt{a^2 + b^2} = \sqrt{8^2 + 6^2} = 10$

Vậy tọa độ các tiêu điểm là (−10; 0), (10; 0)

Tọa độ các đỉnh là (−8; 0), (8; 0)

Độ dài trục thực là: 2a = 2. 8 = 16; độ dài trục ảo là: 2b = 2. 6 = 12.

c) Ta có: x² − 16y² =16 ⇔ $\frac{x^2}{16} – \frac{y^2}{12} = 1$

⇒ a = 4; b = 1 ⇒ c = $\sqrt{a^2 + b^2} = \sqrt{4^2 + 1^2} = \sqrt{17}$

Vậy tọa độ các tiêu điểm là $(-\sqrt{17}; 0), (\sqrt{17}; 0)$

Tọa độ các đỉnh là (−4; 0), (4; 0)

Độ dài trục thực là: 2a = 2. 4 = 8; độ dài trục ảo là: 2b = 2. 1 = 2.

d) Ta có: 9x² − 16y² = 144 => $\frac{x^2}{16} – \frac{y^2}{9} = 1$

⇒ a = 4; b = 3 ⇒ $\sqrt{a^2 + b^2} = \sqrt{4^2 + 3^2} = 5$

Vậy tọa độ các tiêu điểm là (−5; 0), (5; 0)

Tọa độ các đỉnh là (−4; 0), (4; 0).

Độ dài trục thực là: 2a = 2. 4 = 8; độ dài trục ảo là: 2b = 2. 3 = 6.