Bài tập toán lớp 6 Bài 6: Lũy thừa với số mũ tự nhiên

Giải bài tài tập Toán lớp 6 bài 6 có đáp án chi tiết cho từng bài tập trong sách bài tập Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

Bài tập toán lớp 6 bài 6 trang 22

Bài 1.51 trang 22 sách Bài tập toán lớp 6 Tập 1

Viết gọn các tích sau bằng cách dùng lũy thừa:

a) 2. 2. 2. 2. 2;

b) 2. 3. 6. 6. 6;

c) 4. 4. 5. 5. 5.

Hướng dẫn:

a) 2. 2. 2. 2. 2 = 2⁵

b) 2. 3. 6. 6. 6 = 6. 6. 6. 6 = 6⁴

c) 4. 4. 5. 5. 5 = (4. 4). (5. 5. 5) = 4². 5³

Bài 1.52 trang 22 sách Bài tập toán lớp 6 Tập 1

a) Lập bảng giá trị của 2ⁿ với n ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10};

b) Viết dưới dạng lũy thừa của 2 các số sau: 8; 256; 1 024; 2 048.

Hướng dẫn:

a)

+) Với n = 0 thì 2ⁿ = 2⁰ = 1             (theo quy ước)

+) Với n = 1 thì 2ⁿ = 2¹ = 2

+) Với n = 2 thì 2ⁿ = 2² = 2.2 =  4

+) Với n = 3 thì 2ⁿ = 2³= 2.2.2 = 8

+) Với n = 4 thì 2ⁿ = 2⁴ = 2.2.2.2 = 16

+) Với n = 5 thì 2ⁿ = 2⁵ = 2.2.2.2.2 = 32

+) Với n = 6 thì 2ⁿ = 2⁶ = 2.2.2.2.2.2 = 64

+) Với n = 7 thì 2ⁿ = 2⁷ = 2.2.2.2.2.2.2 = 128

+) Với n = 8 thì 2ⁿ = 2⁸ = 2.2.2.2.2.2.2.2 = 256

+) Với n = 9 thì 2ⁿ = 2⁹ = 2.2.2.2.2.2.2.2.2 = 512

+) Với n = 10 thì 2ⁿ = 2¹⁰ = 2.2.2.2.2.2.2.2.2.2 = 1024

Ta có bảng sau:

b) Từ bảng trên ta thấy:

+) 8 = 2³;      256 = 2⁸ ;            1 024 = 2¹⁰;

+) 2 048 = 2. 1 024 = 2¹.2¹⁰ = 2¹⁺¹⁰ = 2¹¹

Bài tập toán lớp 6 bài 6 trang 23

Bài 1.53 trang 23 sách Bài tập toán lớp 6 Tập 1

a) Viết các bình phương của hai mươi số tự nhiên đầu tiên thành một dãy theo thứ tự từ nhỏ đến lớn;

b) Viết các số sau thành bình phương của một số tự nhiên: 64; 100; 121; 169; 196; 289.

Hướng dẫn:

a)

1) Với a = 0 thì a² = 0² = 0.0 = 0

2) Với a = 1 thì a² = 1² = 1.1 = 1

3) Với a = 2 thì a² = 2² = 2.2 = 4

4) Với a = 3 thì a² = 3² = 3.3 = 9

5) Với a = 4 thì a² = 4² = 4.4 = 16

6) Với a = 5 thì a² = 5² = 5.5= 25

7) Với a = 6 thì a² = 6² = 6.6 = 36

8) Với a = 7 thì a² = 7² = 7.7 = 49

9) Với a = 8 thì a² = 8² = 8.8 = 64

10) Với a = 9 thì a² = 9² = 9.9 = 81

11) Với a = 10 thì a² = 10² = 10.10 = 100

12) Với a = 11 thì a² = 11² = 11.11 = 121

13) Với a = 12 thì a² = 12² = 12.12 = 144

14) Với a = 13 thì a² = 13² = 13.13 = 169

15) Với a = 14 thì a² = 14² = 14.14 = 196

16) Với a = 15 thì a² = 15² = 15.15 = 225

17) Với a = 16 thì a² = 16² = 16.16 =  256

18) Với a = 17 thì a² = 17² = 17.17 = 289

19) Với a = 18 thì a² = 18² = 18.18 = 324

20) Với a = 19 thì a² = 19² = 19.19 = 361

Vậy các bình phương của hai mươi số tự nhiên đầu tiên thành một dãy theo thứ tự từ nhỏ đến lớn là: 0; 1; 4; 9; 16; 25; 36; 49; 64; 81; 100; 121; 144; 169; 196; 225; 256; 289; 324; 361.

b)

+) 64 = 8. 8 = 8²

+) 100 = 10. 10 = 10²

+) 121 = 11. 11 = 11²

+) 196 = 14. 14 = 14²

+) 289 = 17. 17 = 17²

Bài 1.54 trang 23 sách Bài tập toán lớp 6 Tập 1

a) Tính nhẩm 10ⁿ với n ∈ {0; 1; 2; 3; 4; 5}. Phát biểu quy tắc tổng quát tính lũy thừa của 10 với số mũ đã cho;

b) Viết dưới dạng lũy thừa của 10 các số sau: 10; 10 000; 100 000; 10 000 000; 1 tỉ.

Hướng dẫn:

a) Ta có:

b) 10 = 10¹; 10 000 = 10⁴; 100 000 = 10⁵; 10 000 000 = 10⁷; 1 tỉ = 1 000 000 000 = 10⁹.

Bài 1.55 trang 23 sách Bài tập toán lớp 6 Tập 1

Tính:

a) 2⁵

b) 5²

c) 2⁴. 3².7

Hướng dẫn:

a) 2⁵= 2.2.2.2.2 = 4.2.2.2 = 8.2.2 = 16.2 = 32

b) 5² = 5. 5 = 25

c) 2⁴. 3².7 = (2. 2. 2. 2). (3.3).7 = (4. 2. 2). 9. 7 = 8. 2. 9. 7 = 16. 9. 7 = 144. 7 = 1 008.

Bài 1.56 trang 23 sách Bài tập toán lớp 6 Tập 1

Tìm n, biết:

a) 5⁴= n

b) n³ = 125

c) 11ⁿ = 1331;

Hướng dẫn:

a) 5⁴ = n;

Hay n = 5⁴ = 5. 5. 5. 5 = 25. 5. 5 = 125. 5 = 625

Vậy n = 625.

b) n³ = 125;

n³ = 5.5.5

n³ = 5³

n = 5

Vậy n = 5.

c) 11ⁿ = 1331

11ⁿ = 11.11.11

11ⁿ = 11³

Vậy n = 3.

Bài 1.57 trang 23 sách Bài tập toán lớp 6 Tập 1

Viết kết quả các phép tính sau dưới dạng một lũy thừa:

a) 3.3⁴.3⁵

b) 7³:7²:7

c) (x⁴)³.

Hướng dẫn:

a) 3.3⁴3⁵= 3¹.3⁴.3⁵=3¹⁺⁴⁺⁵=3¹⁰

^b) 7³:7²:7=7^3-2-1=7⁰=1

c)(x⁴)³=x⁴.x⁴.x⁴=x⁴⁺⁴⁺⁴=x¹²

Bài 1.58 trang 23 sách Bài tập toán lớp 6 Tập 1

Kết luận sau đúng hay sai?

Không có số chính phương nào có chữ số hàng đơn vị là 2.

Hướng dẫn:

Các số tự nhiên có chữ số tận cùng là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 khi bình phương sẽ có chữ số tận cùng lần lượt là 0; 1; 4; 9; 6; 5; 6; 9; 4; 1. Do đó số chính phương bất kì sẽ có chữ số tận cùng là 0; 1; 4; 5; 6; 9.

Vì vậy kết luận không có số chính phương nào có chữ số hàng đơn vị là 2 là đúng.

Bài 1.59 trang 23 sách Bài tập toán lớp 6 Tập 1

Tìm chữ số tận cùng của số 47⁵ và chứng tỏ số 47⁵ + 2021⁶ không phải là số chính phương.

Hướng dẫn:

+) Ta thấy: 47² = 47 . 47 = 47 . (40 + 7) = 47 . 40 + 47. 7 = 47. 40 + (40 + 7) . 7

= 47 . 40 + 40 . 7 + 7 . 7 = 47 . 40 + 40 . 7 + 49

Vì 47 . 40 có chữ số tận cùng là 0; 40 . 7 có chữ số tận cùng là 0; 49 có chữ số tận cùng là 9 nên 472 có chữ số tận cùng của là 0 + 0 + 9 = 9.

Tương tự (47²)² có chữ số tận cùng như chữ số tận cùng của 9² = 81 nên chữ số tận cùng của (47²)² là 1.

Do đó: 47⁵ = 47^{2 + 2 + 1} = 47² . 47² . 47 = (47²)² . 47 có chữ số tận cùng của là 1 . 7 = 7.

Vì vậy chữ số tận cùng của số 47⁵ là 7.

+) Ta có 2 021 có chữ số tận cùng là 1 nên

2 021⁶ = 2 021 . 2 021 . 2 021 . 2 021 . 2 021 . 2 021 có chữ số tận cùng của 1 . 1 . 1 . 1 . 1 . 1 là 1.

Vì vậy chữ số tận cùng của số 2 021⁶ là 1.

Như vậy 47⁵ + 2 021⁶ có chữ số tận cùng là 7 + 1 = 8.

Mà các số tự nhiên thì có chữ số tận cùng là 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 khi bình phương sẽ có chữ số tận cùng lần lượt là 0; 1; 4; 9; 6; 5; 6; 9; 4; 1. Do đó số chính phương bất kì sẽ có chữ số tận cùng là 0; 1; 4; 5; 6; 9.

Vậy 47⁵ + 2 021⁶ có chữ số tận cùng là 8 thì không phải là số chính phương.

Bài 1.60 trang 23 sách Bài tập toán lớp 6 Tập 1

Không tính các lũy thừa, hãy so sánh:

a) 27¹¹ và 81⁸

b) 625⁵ và 125⁷

c) 5³⁶ và 11²⁴

Hướng dẫn:

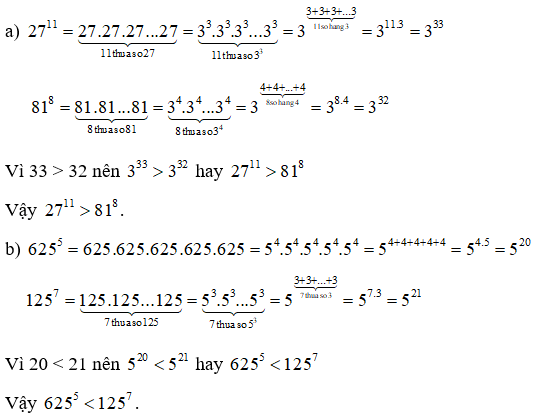
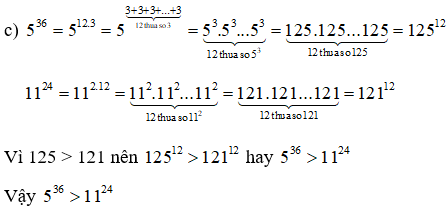
Bài 1.61 trang 23 sách Bài tập toán lớp 6 Tập 1

Giải thích tại sao ba số sau đều là số chính phương:

a) A = 11 – 2

b) B = 1 111 – 22

c) C = 111 111 – 222

Hướng dẫn:

a) A = 11 – 2 = 9 = 3. 3 = 3²

Do đó A là số chính phương.

b) B = 1 111 – 22

= (1 100 + 11) – (11 + 11)

= 1 100 – 11

= 11. 100 – 11. 1

= 11. (100 – 1)

= 11. 99

= 11. (9. 11)

= (11. 11). 9

= (11. 11). (3. 3)

= (11.3). (11. 3)

= 33. 33

= 33²

Do đó B là số chính phương.

c) C = 111 111 – 222

= (111 000 + 111) – (111 + 111)

= 111 000 – 111

= 111. 1 000 – 111. 1

= 111. (1 000 – 1)

= 111. 999

= 111. (111. 9)

= (111. 111). 9

= (111. 111). (3. 3)

= (111. 3). (111. 3)

= 333. 333

= 333²

Do đó C là số chính phương.

Vậy cả ba số A, B, C đều là số chính phương.