Bài tập toán lớp 6 Bài 25: Phép cộng và phép trừ phân số

Giải bài tài tập Toán lớp 6 bài 25 có đáp án chi tiết cho từng bài tập trong sách bài tập Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

Bài tập toán lớp 6 bài 25 trang 11

Bài 6.21 trang 11 sách Bài tập toán lớp 6 Tập 2

Điền số thích hợp vào bảng sau:

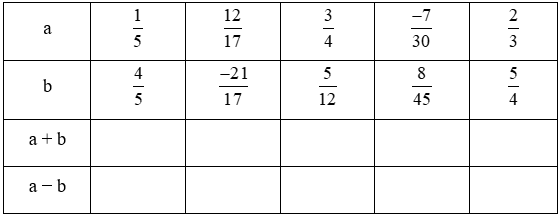
Hướng dẫn:

Ta thực hiện phép cộng và phép trừ ở mỗi cột rồi điền kết quả tính được vào bảng

ta có bảng sau:

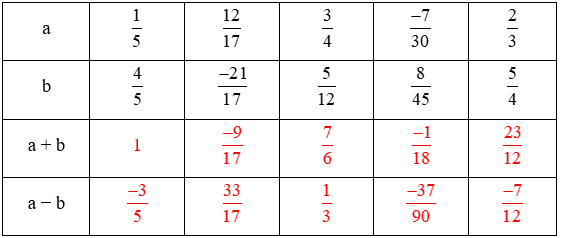
Bài 6.22 trang 11 sách Bài tập toán lớp 6 Tập 2

Thực hiện phép tính:

a) $\frac{3}{4}$+ $\frac{1}{2}$ + $\frac{-3}{32}$

b) $\frac{-5}{7}$- $\frac{3}{8}$ + $\frac{1}{28}$

Hướng dẫn:

a) $\frac{3}{4}$+ $\frac{1}{2}$ + $\frac{-3}{32}$

= $\frac{24}{32}$+ $\frac{16}{32}$ + $\frac{-3}{32}$

= $\frac{37}{32}$

b) $\frac{-5}{7}$- $\frac{3}{8}$ + $\frac{1}{28}$

= $\frac{-40}{56}$- $\frac{21}{56}$ + $\frac{2}{56}$

= $\frac{-59}{56}$

Bài 6.23 trang 11 sách Bài tập toán lớp 6 Tập 2

Hà dự định làm một cái bánh nhỏ. Bạn ấy cần $\frac{3}{4}$ cốc bột mì. Hiện trong túi chỉ còn khoảng $\frac{1}{8}$ cốc bột mì. Hỏi cần thêm bao nhiêu phần cốc bột mì để làm cái bánh đó?

Hướng dẫn:

Lượng bột mì cần bổ sung = Lượng bột mì cần có – Lượng bột mì đã có.

Số phần cốc bột mì cần thêm để làm cái bánh đó là:

$\frac{3}{4}$- $\frac{1}{8}$ = $\frac{6}{8}$- $\frac{1}{8}$ = $\frac{5}{8}$ ( Cốc bột mì)

Vậy cần thêm $\frac{5}{8}$ cốc bột mì để làm cái bánh đó.

Bài tập toán lớp 6 bài 25 trang 12

Bài 6.24 trang 12 sách Bài tập toán lớp 6 Tập 2

Tính một cách hợp lí:

a) A= $\frac{-21}{13}$ + $\frac{8}{11}$ + ( $\frac{-2}{7}$ ) +$\frac{1}{2}$ + $\frac{3}{11}$

b) B= $\frac{11}{17}$ + ( $\frac{-8}{19}$ ) +( $\frac{-3}{4}$ + $\frac{6}{17}$ -$\frac{30}{19}$

Hướng dẫn:

Đối với bài tính một cách hợp lí của biểu thức là tổng của các phân số, ta thường áp dụng tính chất giao hoán, tính chất kết hợp để nhóm các phân số có cùng mẫu số với nhau rồi thực hiện phép tính.

a) A= $\frac{-21}{13}$ + $\frac{8}{11}$ + ( $\frac{-2}{7}$ ) +$\frac{1}{2}$ + $\frac{3}{11}$

= $\frac{-5}{7}$+ $\frac{-2}{7}$ + $\frac{3}{11}$ $\frac{8}{11}$ + $\frac{1}{2}$

=$\frac{-7}{7}$ + $\frac{11}{11}$ + $\frac{1}{2}$

=$\frac{1}{2}$

b) ) B= $\frac{11}{17}$ + ( $\frac{-8}{19}$ ) +( $\frac{-3}{4}$ ) + $\frac{6}{17}$ -$\frac{30}{19}$

= $\frac{11}{17}$+ $\frac{6}{17}$ + ( $\frac{-8}{19}$ ) -$\frac{30}{19}$ +( $\frac{-3}{4}$ )

= $\frac{17}{17}$ + $\frac{-38}{19}$ + $\frac{-3}{4}$

= 1+ (-2) + $\frac{-3}{4}$

= -1+ $\frac{-3}{4}$

=$\frac{-7}{4}$

Bài 6.25 trang 12 sách Bài tập toán lớp 6 Tập 2

Tìm x, biết:

a) $\frac{5}{9}$ -x = $\frac{-3}{9}$

b) x+ $\frac{-7}{13}$= $\frac{-21}{13}$

Hướng dẫn:

a) $\frac{5}{9}$ -x = $\frac{-3}{9}$

🡪x= $\frac{5}{9}$ – $\frac{-3}{9}$

X=$\frac{5+3}{9}$

🡪x= $\frac{8}{9}$

b) x+ $\frac{-7}{13}$= $\frac{-21}{13}$

x= $\frac{-21}{13}$ – $\frac{-7}{13}$

x= $\frac{-14}{13}$

Bài 6.26 trang 12 sách Bài tập toán lớp 6 Tập 2

Ba người cùng làm một công việc. Nếu làm riêng, người thứ nhất mất 6 giờ, người thứ hai mất 5 giờ và người thứ ba mất 7 giờ mới làm xong việc đó. Hỏi nếu ba người cùng làm thì sau một giờ làm được bao nhiêu phần công việc?

Hướng dẫn:

Số phần công việc người thứ nhất làm được trong một giờ là:1 : 6 = $\frac{1}{6}$

Số phần công việc người thứ hai làm được trong một giờ là: 1 : 5 = $\frac{1}{5}$

Số phần công việc người thứ ba làm được trong một giờ là: 1 : 7 = $\frac{1}{7}$

Nếu ba người cùng làm thì sau một giờ làm được số phần công việc là: $\frac{1}{6}$+ $\frac{1}{5}$+$\frac{1}{7}$= $\frac{35}{210}$+ $\frac{42}{210}$+$\frac{30}{210}$= $\frac{107}{210}$ (Công việc)

Vậy nếu ba người cùng làm thì sau một giờ làm được   $\frac{107}{210}$công việc.

Bài 6.27 trang 12 sách Bài tập toán lớp 6 Tập 2

Nhân dịp nghỉ lễ, Việt cùng gia đình đi nghỉ mát ở Đà Nẵng. Họ đi bằng xe khách từ Hà Nội đến thành phố Đồng Hới (Quảng Bình) hết $9\frac{1}{4}$  giờ, sau đó họ nghỉ ngơi một lúc, rồi tiếp tục hành trình đi từ thành phố Đồng Hới đến Đà Nẵng hết $5\frac{1}{8}$  giờ. Hỏi gia đình Việt đi hết bao nhiêu thời gian từ Hà Nội đến Đà Nẵng?

Hướng dẫn:

Ta có $\frac{1}{4}$ = $\frac{9.4+1}{4}$ =$\frac{37}{4}$ ; $5\frac{1}{8}$= $\frac{5.8+1}{8}$=$\frac{41}{8}$

Gia đình Việt đi từ Hà Nội đến Đà Nẵng hết thời gian là: $9\frac{1}{4}$+ $5\frac{1}{8}$= $\frac{37}{4}$ + $\frac{41}{8}$ = $\frac{115}{8}$ =$14\frac{3}{8}$

Vậy gia đình Việt đi hết $14\frac{3}{8}$ giờ từ Hà Nội đến Đà Nẵng.

Bài 6.28 trang 12 sách Bài tập toán lớp 6 Tập 2

Tính chu vi của một tam giác biết độ dài các cạnh của tam giác là $2\frac{1}{2}$ cm; $3\frac{3}{5}$ cm ; $4\frac{1}{6}$ cm

Hướng dẫn:

$2\frac{1}{2}$= $\frac{2.2+1}{2}$=$\frac{5}{2}$

$3\frac{3}{5}$=$\frac{3.5+3}{5}$= $\frac{18}{5}$

$4\frac{1}{6}$ = $\frac{4.6+1}{6}$= $\frac{25}{6}$

Chu vi của tam giác đó là: $2\frac{1}{2}$ + $3\frac{3}{5}$ +$4\frac{1}{6}$ cm = $\frac{5}{2}$+$\frac{18}{5}$ +$\frac{25}{6}$ = $\frac{154}{15}$ =$10\frac{4}{15}$ (cm )

Vậy chu vi của tam giác đó là $10\frac{4}{15}$ (cm)

Chú ý: Ngoài ra, để thực hiện phép cộng các hỗn số, ta có thể tách phần số nguyên và phần phân số của hai hỗn số, rồi thực hiện cộng các phần số nguyên với nhau, các phần phân số với nhau. Ta được:

$2\frac{1}{2}$ + $3\frac{3}{5}$+ $4\frac{1}{6}$ =2+ $\frac{1}{2}$+3 + $\frac{3}{5}$+4 + $\frac{1}{6}$

= (2+3+4) + ( $\frac{1}{2}$ + $\frac{3}{5}$ + $\frac{1}{6}$ )

= 9+ $\frac{19}{15}$= $10\frac{4}{15}$

Bài 6.29 trang 12 sách Bài tập toán lớp 6 Tập 2

Em hãy điền phân số thích hợp vào ô trống để hoàn thiện sơ đồ sau, biết số trong mỗi ô trống ở hàng trên bằng tổng của hai số kề nó ở hàng dưới.

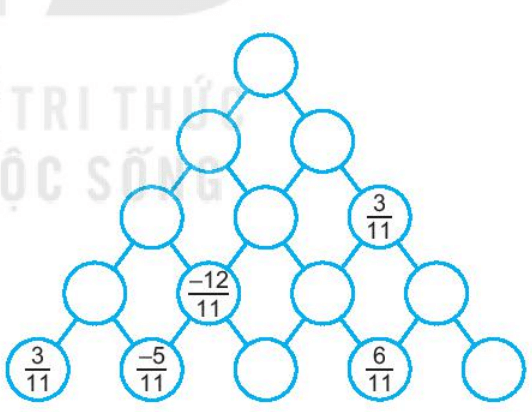
Hướng dẫn:

Mỗi ô trống ở hàng trên bằng tổng của hai số kề nó ở hàng dưới. Ta thực hiện lần lượt các ô còn lại dựa vào các ô đã biết như sau:

$\frac{3}{11}$ + $2\frac{-5}{11}$ = $\frac{-2}{11}$

$\frac{-2}{11}$ + $\frac{-12}{11}$ = $\frac{-14}{11}$

$\frac{-12}{11}$- $\frac{-5}{11}$ = $\frac{-7}{11}$

$\frac{-7}{11}$+ $\frac{6}{11}$ = $\frac{-1}{11}$

$\frac{-12}{11}$+ $\frac{-1}{11}$ = $\frac{-13}{11}$

$\frac{-14}{11}$+ $\frac{-13}{11}$ = $\frac{-27}{11}$

$\frac{6}{11}$+ $\frac{-2}{11}$ = $\frac{4}{11}$

$\frac{-1}{11}$+ $\frac{4}{11}$ = $\frac{3}{11}$

$\frac{-13}{11}$+ $\frac{3}{11}$ = $\frac{-10}{11}$

$\frac{-27}{11}$+ $\frac{-10}{11}$ = $\frac{-37}{11}$

Vậy ta điền vào các ô còn trống như sau:

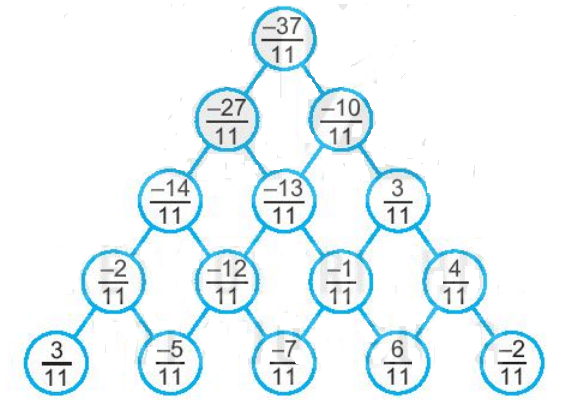
Bài 6.30 trang 12 sách Bài tập toán lớp 6 Tập 2

Đây là mẩu giấy duy nhất còn sót lại của một tài liệu.

Em hãy khôi phục lại ba dòng trên và ba dòng tiếp theo của tài liệu theo quy luật các phép tính của ba dòng còn lại.

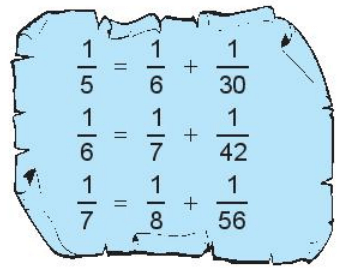
Hướng dẫn:

Xét ba hàng còn sót lại của mẩu giấy, ta thấy:

– Hàng thứ nhất: $\frac{1}{5}$= $\frac{1}{6}$+$\frac{1}{30}$= $\frac{1}{5+1}$+$\frac{1}{5.(5+1)}$

– Hàng thứ hai: $\frac{1}{6}$=$\frac{1}{7}$+$\frac{1}{42}$=$\frac{1}{6+1}$+ $\frac{1}{6.(6+1)}$

– Hàng thứ ba: $\frac{1}{7}$= $\frac{1}{8}$+$\frac{1}{56}$= $\frac{1}{7+1}$ +$\frac{1}{7.(7+1)}$

Quy luật của phép tính này là: $\frac{1}{n}$ = $\frac{1}{n+1}$+ $\frac{1}{n.(n+1)}$  (với n là số tự nhiên khác 0).

Dựa vào quy luật trên ta tính đuợc các dòng khác như sau:

– Ba dòng tài liệu trên là:

$\frac{1}{2}$= $\frac{1}{2+1}$+ $\frac{1}{2.(2+1)}$= $\frac{1}{3}$+ $\frac{1}{6}$

$\frac{1}{3}$= $\frac{1}{3+1}$+ $\frac{1}{3.(3+1)}$= $\frac{1}{4}$+ $\frac{1}{12}$

$\frac{1}{4}$= $\frac{1}{4+1}$+ $\frac{1}{4.(4+1)}$= $\frac{1}{5}$+ $\frac{1}{20}$

– Ba dòng tài liệu tiếp theo là:

$\frac{1}{8}$= $\frac{1}{8+1}$+ $\frac{1}{8.(8+1)}$= $\frac{1}{9}$+ $\frac{1}{72}$

$\frac{1}{9}$= $\frac{1}{9+1}$+ $\frac{1}{9.(9+1)}$= $\frac{1}{10}$+ $\frac{1}{90}$

$\frac{1}{10}$= $\frac{1}{10+1}$+ $\frac{1}{10.(10+1)}$= $\frac{1}{11}$+ $\frac{1}{110}$

Vậy:

– Ba dòng tài liệu trên là:

$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$

$\frac{1}{3}$=$\frac{1}{4}$ + $\frac{1}{12}$

$\frac{1}{4}$ = $\frac{1}{5}$ + $\frac{1}{20}$

– Ba dòng tài liệu tiếp theo là:

$\frac{1}{8}$=$\frac{1}{9}$+$\frac{1}{72}$

$\frac{1}{9}$= $\frac{1}{10}$+$\frac{1}{90}$

$\frac{1}{10}$= $\frac{1}{11}$+ $\frac{1}{110}$