Bài tập toán lớp 6 Bài 26. Phép nhân và phép chia phân số
Bài tập toán lớp 6 Bài 26. Phép nhân và phép chia phân số
Giải bài tài tập Toán lớp 6 bài 26 có đáp án chi tiết cho từng bài tập trong sách bài tập Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.
Bài tập toán lớp 6 bài 26 trang 14
Bài 6.31 trang 14 sách Bài tập toán lớp 6 Tập 2
Điền các số thích hợp vào bảng sau:
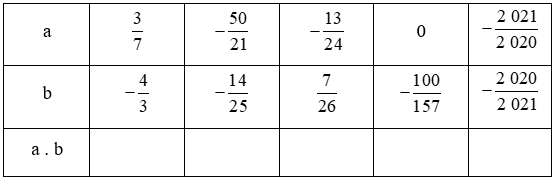
Hướng dẫn:
Thực hiện phép nhân lần lượt từng cột như sau:
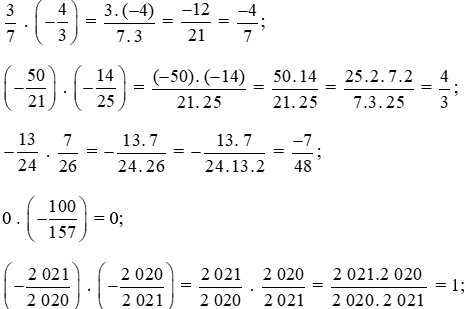
Vậy ta điền các số vào bảng như sau:
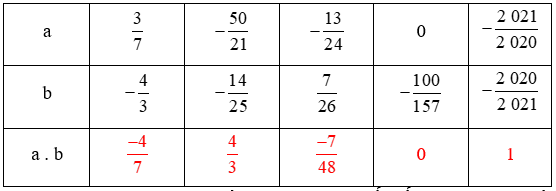
Bài 6.32 trang 14 sách Bài tập toán lớp 6 Tập 2
Điền các số thích hợp vào bảng sau:
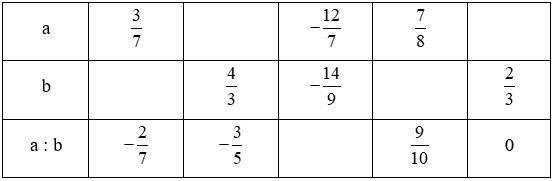
Hướng dẫn:
Thực hiện phép tính lần lượt từng cột như sau:
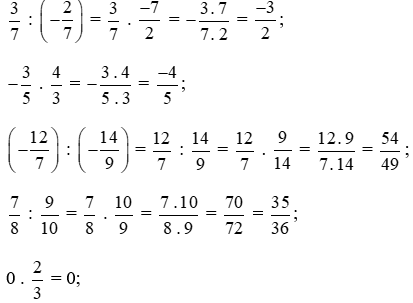
Ta điền các số vào bảng như sau:
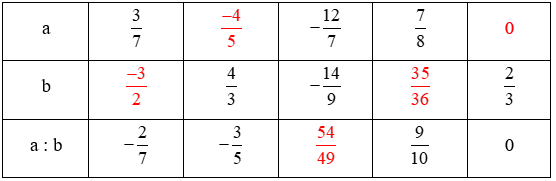
Bài tập toán lớp 6 bài 26 trang 15
Bài 6.33 trang 15 sách Bài tập toán lớp 6 Tập 2
Tính giá trị của các biểu thức sau:
A= $\frac{-9}{10}$ $\frac{7}{11}$. $\frac{10}{9}$.(-22)
B= $\frac{-5}{7}$.$\frac{6}{13}$.$\frac{-7}{5}$.(-39)
Hướng dẫn:

Bài 6.34 trang 15 sách Bài tập toán lớp 6 Tập 2
Người ta ước tính rằng tổng lượng nước trên Trái Đất là khoảng 1 380 triệu km3, trong đó khoảng$\frac{97}{100}$ lượng nước là nước mặn (không uống được) và $\frac{3}{100}$ lượng nước là nước ngọt. Trong $\frac{3}{100}$ lượng nước ngọt thì có khoảng $\frac{2}{3}$ lượng nước này tồn tại ở dạng sông băng và các mũ băng ở các cực, $\frac{1}{3}$ lượng nước này tồn tại ở dạng nước ngầm và bề mặt Trái Đất. Hãy ước tính lượng nước ngầm và bề mặt Trái Đất.
(Theo www.worldwater.org)

Hướng dẫn:
Đổi: 1 380 triệu km3 = 1 380 000 km3
Lượng nước ngọt trên Trái Đất là:
1 380 000 000. $\frac{3}{100}$ = 41 400 000 (km3)
Lượng nước nước ngầm và bề mặt Trái Đất là:
41 400 000 . $\frac{1}{3}$ = 13 800 000 (km3)
Vậy lượng nước nước ngầm và bề mặt Trái Đất là 13 800 000 km3.
Bài 6.35 trang 15 sách Bài tập toán lớp 6 Tập 2
Hiện nay, khoảng $\frac{2}{5}$ diện tích đất của Việt Nam được che phủ bởi rừng. Có khoảng $\frac{7}{10}$ diện tích rừng tự nhiên, còn lại là rừng trồng.
Hỏi:
a) Diện tích rừng tự nhiên bằng mấy phần diện tích đất của Việt Nam?
b) Diện tích rừng tự nhiên bằng mấy phần diện tích rừng trồng?
(Theo Tổng cục Thống kê)
Hướng dẫn:
a) Diện tích rừng tự nhiên bằng số phần diện tích đất của Việt Nam là: $\frac{2}{5}$ . $\frac{7}{10}$ = $\frac{14}{50}$ =$\frac{7}{25}$
Vậy diện tích rừng tự nhiên bằng $\frac{7}{25}$ diện tích đất của Việt Nam.
b) Diện tích rừng trồng bằng số phần diện tích rừng là:
1-$\frac{7}{10}$= $\frac{3}{10}$
Diện tích rừng tự nhiên bằng số phần diện tích rừng trồng là:
$\frac{7}{10}$: $\frac{3}{10}$= $\frac{7}{3}$
Vậy diện tích rừng tự nhiên bằng $\frac{7}{3}$ diện tích rừng trồng.
Bài 6.36 trang 15 sách Bài tập toán lớp 6 Tập 2
Tính giá trị của các biểu thức sau:
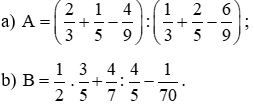
Hướng dẫn:

Bài 6.37 trang 15 sách Bài tập toán lớp 6 Tập 2
Tính một cách hợp lí:
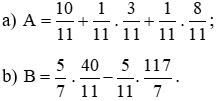
Hướng dẫn:

Bài tập toán lớp 6 bài 26 trang 16
Bài 6.38 trang 16 sách Bài tập toán lớp 6 Tập 2
Vào buổi sáng Chủ nhật, hai bạn Tuấn và Hà cùng đi bộ quanh Hồ Gươm. Lúc 6 giờ 30 phút, bạn Tuấn bắt đầu đi từ đền Ngọc Sơn với vận tốc 4 km/h. Lúc 6 giờ 35 phút, bạn Hà cũng bắt đầu đi từ đền Ngọc Sơn với vận tốc $\frac{9}{2}$ km/h, nhưng theo chiều ngược lại. Hai bạn gặp nhau ở Bưu điện Hà Nội lúc 6 giờ 45 phút.
Tính độ dài quãng đường đi bộ một vòng quanh Hồ Gươm.
Hướng dẫn:
Thời gian bạn Tuấn đi từ khi bắt đầu đến khi gặp nhau là: 6 giờ 45 phút- 6 giờ 30 phút = 15 phút = $\frac{1}{4}$ (giờ)
Thời gian bạn Hà đi từ khi bắt đầu đến khi gặp nhau là: 6 giờ 45 phút – 6 giờ 35 phút = 10 phút= $\frac{1}{6}$
Quãng đường bạn Tuấn đã đi được là:
4. $\frac{1}{4}$ = 1 (km)
Quãng đường bạn Hà đã đi được là:
$\frac{9}{2}$ . $\frac{1}{6}$ =$\frac{3}{4}$ (km)
Độ dài quãng đường đi bộ một vòng quanh Hồ Gươm bằng tổng quãng đường Tuấn và Hà cho đến khi gặp nhau và bằng:
1+ $\frac{3}{4}$= $\frac{7}{4}$
Vậy độ dài quãng đường đi bộ một vòng quanhh Hồ Gươm là $\frac{7}{4}$ km.
Bài 6.39 trang 16 sách Bài tập toán lớp 6 Tập 2
Theo một ngiên cứu của các nhà khoa học Mĩ (American College of Sport Medicine), đối với người hoạt động bình thường, lượng nước (theo đơn vị mililít) cần cung cấp cho cơ thể trong một ngày được tính theo công thức:
CÂN NẶNG (theo đơn vị kg) × 30
Đối với người tập thể dục, bạn cần uống thêm khoảng 355 ml nước cho mỗi 30 phút trong khi luyện tập. Hỏi với một người nặng 60 kg, tập thể dục trong 60 phút mỗi ngày thì cần uống khoảng bao nhiêu lít nước mỗi ngày?
(Theo suckhoegiadinh.com.vn)
Hướng dẫn:
Lượng nước cần cung cấp cho cơ thể đối với người hoạt động bình thường là:
60 . 30 = 1 800 (ml)
Lượng nước cần uống thêm khi tập thể dục là:
355 . (60 : 30) = 710 (ml)
Tổng lượng nước cần dùng là:
1 800 + 710 = 2 510 (ml) = 2,51 (l)
Vậy với một người nặng 60 kg, tập thể dục trong 60 phút mỗi ngày thì cần uống khoảng 2,5 lít.
Bài 6.40 trang 16 sách Bài tập toán lớp 6 Tập 2
Tính giá trị của biểu thức:
![]()
Hướng dẫn:

Bài 6.41 trang 16 sách Bài tập toán lớp 6 Tập 2
Tìm số đo còn thiếu trong các hình sau:

Hướng dẫn:
Diện tích hình tam giác = $\frac{1}{2}$ độ dài cạnh đáy . chiều cao tương ứng với cạnh đáy đó.
Diện tích hình vuông = Độ dài một cạnh . độ dài một cạnh.
Hình a) là hình tam giác có độ dài cạnh đáy là $\frac{11}{4}$. cm và chiều cao tương ứng là $\frac{14}{5}$. cm.
Diện tích hình tam giác là:
$\frac{1}{2}$.$\frac{11}{4}$ . $\frac{14}{5}$ =$\frac{77}{20}$ (cm2)
Hình b) là hình vuông có diện tích $\frac{81}{16}$. cm2.
Ta thấy 81=9.9; 16=4.4 nên $\frac{81}{16}$ = $\frac{9}{4}$. $\frac{9}{4}$
Do đó độ dài một cạnh của hình vuông ở Hình b) là $\frac{9}{4}$ cm.
Vậy số đo còn thiếu ở Hình a) là$\frac{77}{20}$ và Hình b) là $\frac{9}{4}$.
