Bài tập toán lớp 6 Bài 29. Tính toán với số thập phân

Giải bài tài tập Toán lớp 6 bài 29 có đáp án chi tiết cho từng bài tập trong sách bài tập Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

Bài tập toán lớp 6 bài 29 trang 27

Bài 7.8 trang 27 sách Bài tập toán lớp 6 Tập 2

Thực hiện phép tính:

a) 34,25 – 78,43;

b) 65,19 + (–81,14);

c) (–2,25) + 7,63;

d) (–81,2) + (–17,5);

e) (–2,71) – (–27,3);

f) (–98,2) + 3,51.

Hướng dẫn:

a) 34,25 – 78,43 = 34,25 + (–78,43) = –(78,43 – 34,25) = –44,18;

b) 65,19 + (–81,14)= –(81,14 – 65,19) = –15,95;

c) (–2,25) + 7,63 = 7,63 – 2,25 = 5,38;

d) (–81,2) + (–17,5) = –(81,2 + 17,5) = –98,7;

e) (–2,71) – (–27,3) = –2,71 + 27,3 = 27,3 –2,71 = 24,59;

f) (–98,2) + 3,51 = –(98,2 – 3,51) = –94,69.

Bài 7.9 trang 27 sách Bài tập toán lớp 6 Tập 2

Thực hiện phép tính:

a) (–35,3) . 4,1;

b) 2,9 . (–5,4);

c) (–3,25) . (–0,21);

d) (–8,058) : 3,4;

e) (–4,725) : (–1,5);

f) 82,28 : (–4,4).

Hướng dẫn:

a) (–35,3) . 4,1 = –(35,3 . 4,1) = –144,73;

b) 2,9 . (–5,4) = –(2,9 . 5,4) = –15,66;

c) (–3,25) . (–0,21) = –(3,25 . 0,21) = 0,6825;

d) (–8,058) : 3,4 = –(8,058 : 3,4) = –2,37;

e) (–4,725) : (–1,5) = 4,725) : 1,5 = 3,15;

f) 82,28 : (–4,4) = –(82,28 : 4,4) = –18,7.

Bài 7.10 trang 27 sách Bài tập toán lớp 6 Tập 2

Tính nhẩm

a) (–32,5) . 0,01;

b) (–4,512) : (–0,001);

c) (–2,378) : 0,1;

d) 125,03 . (–0,1).

Hướng dẫn:

Quy tắc:

– Khi nhân một số thập phân với 0,1; 0,01; 0,001 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.

– Khi chia một số thập phân cho 0,1; 0,01; 0,001 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, … chữ số.

a) (–32,5) . 0,01 = –(32,5 . 0,01) = –0,325;

b) (–4,512) : (–0,001) = 4,512 : 0,001 = 4512;

c) (–2,378) : 0,1 = –(2,378 : 0,1) = –23,78;

d) 125,03 . (–0,1) = –(125,03 . 0,1) = –12,503.

Bài 7.11 trang 27 sách Bài tập toán lớp 6 Tập 2

Sử dụng quy tắc dấu ngoặc tính các tổng sau:

a) (–8,5) + 16,35+ (–4,5) – (–2,25);

b) 5,63 + (–2,75) – (–8,94) + 9,06 – 15,25.

Hướng dẫn:

Đối với bài toán tính tổng các số hạng, ta thường áp dụng các tính chất giao hoán, kết hợp để đưa các về các nhóm có tổng là số nguyên để tiện cho việc tính toán.

a) (–8,5) + 16,35+ (–4,5) – (–2,25)

= (–8,5) + 16,35+ (–4,5) + 2,25 (Quy tắc bỏ ngoặc)

= [(–8,5) + (–4,5)] + (16,35 + 2,25) (Tính chất kết hợp)

= –13 + 18,6

= 18,6 –13

= 5,6.

b) 5,63 + (–2,75) – (–8,94) + 9,06 – 15,25

= 5,63+ (–2,75) + 8,94 + 9,06 + (–15,25)  (Quy tắc bỏ ngoặc)

= [(–2,75) + (–15,25)] + (8,94 + 9,06) + 5,63 (Tính chất kết hợp)

= –18 + 18 + 5,63

= 0 + 5,63

= 5,63.

Bài 7.12 trang 28 sách Bài tập toán lớp 6 Tập 2

a) 35,5 . 35,5 + 71. 64,5 + 64,5 . 64,5;

b) 8,5 . 8,5 – 2. 8,5 . 3,5 + 3,5 . 3,5.

Hướng dẫn:

Đối với bài toán có chứa phép cộng (trừ) và phép nhân, ta thường sử dụng tính chất phân phối để tính giá trị biểu thức một cách hợp lí.

a) 35,5 . 35,5 + 71. 64,5 + 64,5 . 64,5

= 35,5 . 35,5 + 2. 35,5. 64,5 + 64,5 . 64,5

= 35,5. 35,5 + (35,5 + 35,5). 64,5 + 64,5 . 64,5

= 35,5. 35,5 + 35,5. 64,5 + 35,5. 64,5 + 64,5 . 64,5 (Tính chất phân phối)

= (35,5. 35,5 + 35,5. 64,5) + (35,5. 64,5 + 64,5 . 64,5) (Tính chất kết hợp)

= 35,5. (35,5 + 64,5) + 64,5. (35,5 + 64,5) (Tính chất phân phối)

= 35,5 . 100 + 64,5 . 100

= 100. (35,5 +64,5) (Tính chất phân phối)

= 100 . 100

= 10 000.

b) 8,5 . 8,5 – 2. 8,5 . 3,5 + 3,5 . 3,5

= 8,5 . 8,5 – (8,5 + 8,5) . 3,5 + 3,5 . 3,5

= 8,5 . 8,5 – (8,5 . 3,5 + 8,5 . 3,5) + 3,5 . 3,5 (Tính chất phân phối)

= 8,5. 8,5 – 8,5. 3,5 – 8,5. 3,5 + 3,5. 3,5

= (8,5. 8,5 – 8,5. 3,5) – (8,5. 3,5 – 3,5. 3,5)

= 8,5. (8,5 – 3,5) – 3,5. (8,5 – 3,5)

= 8,5 . 5 – 3,5 . 5 (Tính chất phân phối)

= 5. (8,5 – 3,5)  (Tính chất phân phối)

= 5 . 5 = 25.

Bài tập toán lớp 6 bài 29 trang 28

Bài 7.13 trang 28 sách Bài tập toán lớp 6 Tập 2

Tính giá trị của biểu thức:

a) 0,125 . 351 + (–35,1) : 4;

b) (–20) . 3,1 – 7,2 : 4 + 3,1 . (4,5 . 6 – 5,2);

c) (x + 13,67) . (–10) + 136,7 tại x = –1,26.

Hướng dẫn:

a) 0,125 . 351 + (–35,1) : 4

= 0,125 . 351 – 351 . 0, 025

= 351. (0,125 – 0,025) (Tính chất phân phối)

= 351 . 0,1

= 35,1.

b) (–20) . 3,1 – 7,2 : 4 + 3,1 . (4,5 . 6 – 5,2)

= (–20) . 3,1 + 3,1 . (4,5 . 6 – 5,2) – 7,2 : 4 (Tính chất giao hoán)

= 3,1 . [(–20) + 4,5. 6 – 5,2] – 7,2 : 4 (Tính chất phân phối)

= 3,1 . 1,8 – 1,8

= 1,8 . (3,1 – 1)

=1,8 . 2,1

= 3,78.

c) (x + 13,67) . (–10) + 136,7

Thay x = –1,26 vào biểu thức ta được:

= (–1,26) . (–10) + 13,67. (–10) + 136,7

= 12,6 + (–136,7) + 136,7

= 12,6 + [(–136,7) + 136,7] (Tính chất kết hợp)

= 12,6 + 0

= 12,6.

Bài 7.14 trang 28 sách Bài tập toán lớp 6 Tập 2

Ba nước Mĩ, A-rập Xê-út và Nga đứng đầu thế giới về sản xuất dầu thô, đạt sản lượng trung bình lần lượt là 15,043; 12; 10,08 triệu thùng dầu mỗi ngày. Em hãy cho biết mỗi ngày cả ba nước này sản xuất được bao nhiêu thùng dầu.

Hướng dẫn:

Mỗi ngày cả ba nước này sản xuất được:

15,043 + 12 + 10,08 = 37,123 (triệu thùng) = 37 123 000 (thùng)

Vậy mỗi ngày cả ba nước này sản xuất được 37 123 000 thùng dầu.

Bài 7.15 trang 28 sách Bài tập toán lớp 6 Tập 2

Một hộ gia đình đem 140 kg muối ăn đóng thành các túi, mỗi túi đựng được 0,8 kg muối. Hỏi hộ gia đình đó đóng được bao nhiêu túi muối ăn?

Hướng dẫn:

Số túi muối ăn hộ gia đình đó đóng được là:

140 : 0,8 = 175 (túi)

Vậy hộ gia đình đó đóng được 175 túi muối ăn.

Bài 7.16 trang 28 sách Bài tập toán lớp 6 Tập 2

Bảng bên cho biết thông tin dự báo thời tiết tại thành phố Hà Nội ngày 29-12-2020 và 5 ngày tiếp theo trong tuần hiển thị trên màn hình một chiếc điện thoại. Nhiệt độ được ghi bằng đơn vị độ F (Fahrenheit). Công thức đổi đơn vị độ F sang độ C là:

C = (F – 32) : 1,8;

với F: nhiệt độ ghi bằng độ F,

C: nhiệt độ ghi bằng độ C tương ứng.

Chẳng hạn, nhiệt độ cao nhất trong ngày 29-12-2020 tại Hà Nội là 81^oF, tức là:

(81 – 32) : 1,8 ≈ 27^oC.

a) Nhiệt độ thấp nhất trong ngày 29-12-2020 tại Hà Nội là bao nhiêu độ C?

b) Dự báo nhiệt độ cao nhất, thấp nhất tại Hà Nội vào thứ Sáu, ngày 01-01-2021 là bao nhiêu độ C (sử dụng máy tính cầm tay rồi lấy kết quả đến chữ số hàng đơn vị).

Hướng dẫn:

a) Dựa vào bảng trên, nhiệt độ thấp nhất trong ngày 29-12-2020 tại Hà Nội là 59^oF.

Thay F = 59 vào biểu thức (F – 32) : 1,8 ta tính được:

Nhiệt độ thấp nhất trong ngày 29-12-2020 tại Hà Nội là:

(59 – 32) : 1,8 = 15 (^oC)

Vậy nhiệt độ thấp nhất trong ngày 29-12-2020 tại Hà Nội là 15 ^oC.

b) Dựa vào bảng trên, nhiệt độ thấp nhất trong ngày 01-01-2021 tại Hà Nội là 63^oF.

Thay F = 63 vào biểu thức (F – 32) : 1,8 ta tính được:

Nhiệt độ dự báo thấp nhất trong ngày 01-01-2021 tại Hà Nội là:

(63 – 32) : 1,8 ≈ 17(^oC)

Dựa vào bảng trên, nhiệt độ cao nhất trong ngày 01-01-2021 tại Hà Nội là 45^oF.

Thay F = 45 vào biểu thức (F – 32) : 1,8 ta tính được:

Nhiệt độ dự báo cao nhất trong ngày 01-01-2021 tại Hà Nội là:

(45 – 32) : 1,8 ≈ 7(^oC)

Vậy nhiệt độ cao nhất và thấp nhất tại Hà Nội vào ngày thứ Sáu, ngày 01-01-2021 lần lượt là 17^oC và 7^oC.

Bài 7.17 trang 28 sách Bài tập toán lớp 6 Tập 2

Điền chữ số thích hợp vào ô trống:

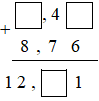
Hướng dẫn:

Vì số chữ số ở phần thập phân của các số đều như nhau nên ta có thể bỏ đi dấu phẩy ở các số như sau:

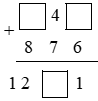
Ta đưa bài toán về: Tìm các chữ số a, b, c sao cho $\overline{a4b}$ + 876 = $\overline{12c1}$ (a,b,c ∈ N; 0<a ≤9 ; 0 ≤ b, c≤9)

Ta thấy b + 6 có tận cùng là 1, mà 0 ≤ b, c≤ 9 ,b ∈ N

nên b + 6 = 11.

Do đó, b = 5.

Khi đó, $\overline{a45}$ + 876= $\overline{12cl}$

100a + 40 + 5 + 876 = 1200 + 10c +1

100a + 921 = 10c + 1201

100a = 10c + 1201 – 921

100a = 10c + 280

10a = c + 28

Do đó (c  + 28) là bội của 10 hay (c  + 28) có tận cùng là 0. Mà 0 ≤c≤ 9, c ∈ N

nên c = 2 suy ra c  + 28 = 30.

Do đó 10a = 30 suy ra a = 3.

Từ đó suy ra a = 3, b = 5, c = 2.

Vậy chữ số thích hợp điền vào ô trống như sau: