Bài 4: Ôn tập và bổ sung về phân số (SGK toán lớp 5 trang 12,13,14)

Với lời giải bài 4 SGK toán lớp 5 trang 12 cánh diều tập 1. Hi vọng sẽ là tài liệu tham khảo cho quý phụ huynh và học sinh hiểu rõ phương pháp giải toán lớp 5 Cánh diều

1. SGk Toán lớp 5 trang 12

1.1 Toán lớp 5 trang 12 Bài 1

Trò chơi “Ghép thẻ”

a) Ghép các thẻ ghi phân số thích hợp với thẻ hình vẽ có số phần đã tô màu tương ứng:

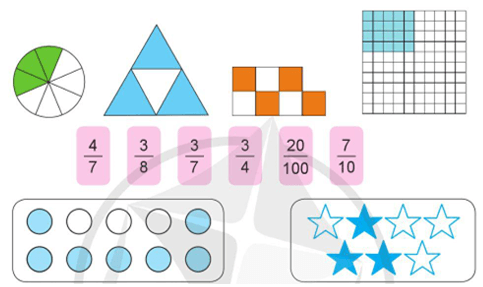
b) Đọc các phân số ở câu a và nêu tử số, mẫu số của mỗi phân số đó.

Hướng dẫn giải:

a)

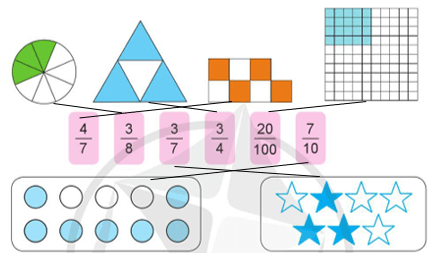
b)

$\frac{4}{7}$ đọc là: bốn phần bảy; tử số là 4, mẫu số là 7

$\frac{3}{8}$ đọc là: ba phần tám; tử số là 3, mẫu số là 8

$\frac{3}{7}$ đọc là: ba phần bảy; có tử số là 3, mẫu số là 7

$\frac{3}{4}$đọc là: ba phần tư; tử số là 3, mẫu số là 4

$\frac{20}{100}$ đọc là: hai mươi phần một trăm; tử số là 20, mẫu số là 100

$\frac{7}{10}$ đọc là: bảy phần mười; tử số là 7, mẫu số là 10

1.2 Toán lớp 5 trang 12 Bài 2

a) Viết phân số chỉ số phần đã tô màu trong mỗi hình rồi đọc (theo mẫu):

Hướng dẫn giải:

a)

a) Hình A

Viết $\frac{42}{100}$

Đọc: Bốn mươi hai phần một trăm hay bốn mươi hai phần trăm

b) Hình B

Viết $\frac{6}{100}$

Đọc: Sáu phần một trăm hay sáu phần trăm

c) Hình C

$\frac{27}{1000}$

Đọc: Hai mươi bảy phần một nghìn hay hai bảy phần nghìn

d) Hình D

$\frac{65}{1000}$

Đọc: Sáu mươi lăm phần một nghìn hay sáu mươi lăm phần nghìn

b)

11 : 5 = $\frac{11}{5}$

9 : 100 = $\frac{9}{100}$

33 : 30 = $\frac{33}{30}$

c) Viết các số tự nhiên sau thành phân số (theo mẫu):

Mẫu: 4 = $\frac{4}{1}$

301 = $\frac{301}{1}$

12 = $\frac{12}{1}$

2 025 = $\frac{2025}{1}$

2. SGK Toán lớp 5 trang 13

2.1 Toán lớp 5 trang 13 Bài 3

a) Nêu hai phân số bằng mỗi phân số sau: $\frac{5}{4}$; $\frac{9}{12}$.

b) Rút gọn các phân số sau: $\frac{24}{32}$; $\frac{14}{35}$;$\frac{30}{25}$; $\frac{63}{36}$

Hướng dẫn giải:

a) $\frac{5}{4}$= $\frac{5×3}{4×3}$= $\frac{15}{12}$; $\frac{5}{4}$=$\frac{5×5}{4×5}$=$\frac{25}{20}$

Hai phân số bằng phân số $\frac{5}{4}$ là $\frac{15}{12}$ và $\frac{25}{20}$

$\frac{9}{12}$=$\frac{9:3}{12:3}$=$\frac{3}{4}$;$\frac{9}{12}$=$\frac{9×2}{12×2}$=$\frac{18}{24}$

Hai phân số bằng phân số là $\frac{9}{12}$là $\frac{3}{4}$và $\frac{18}{24}$

b)  $\frac{24}{32}$=$\frac{24:8}{32:8}$=$\frac{3}{4}$

$\frac{14}{35}$=$\frac{14:7}{35:7}$=$\frac{2}{5}$

$\frac{30}{25}$=$\frac{30:5}{25:5}$=$\frac{6}{5}$

$\frac{63}{36}$=$\frac{63:9}{36:9}$=$\frac{7}{4}$

2.2 Toán lớp 5 trang 13 Bài 4

Quy đồng mẫu số hai phân số:

Hướng dẫn giải:

a)  $\frac{4}{7}$=$\frac{4×2}{7×2}$=$\frac{8}{14}$; giữ nguyên phân số  $\frac{3}{14}$.

Vậy quy đồng mẫu số hai phân số $\frac{3}{14}$và $\frac{4}{7}$ ta được $\frac{3}{14}$ và $\frac{8}{14}$.

b)  $\frac{2}{3}$=$\frac{2×2}{3×2}$= $\frac{4}{6}$; giữ nguyên phân số $\frac{5}{6}$.

Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$và $\frac{5}{6}$ ta được $\frac{4}{6}$ và $\frac{5}{6}$.

2.3 Toán lớp 5 trang 13 Bài 5

a) Đọc ví dụ sau rồi nói cho bạn nghe cách thực hiện:

Ví dụ: Quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{5}{4}$

Vì 3 x 4 = 12 nên ta chọn 12 làm mẫu số chung.

Ta có: $\frac{2}{3}$=$\frac{2×4}{3×4}$=$\frac{8}{12}$ và $\frac{5}{4}$ =$\frac{5×3}{4×3}$=$\frac{15}{12}$

Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$ và  $\frac{5}{4}$ ta được  $\frac{8}{12}$ và  $\frac{15}{12}$

b) Quy đồng mẫu số hai phân số:

Hướng dẫn giải: 

a) Cách quy đồng mẫu số:

– Chọn mẫu số chung

– Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

– Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

b) $\frac{1}{4}$ và $\frac{5}{3}$

Vì 4 x 3 = 12 nên ta chọn 12 làm mẫu số chung.

Ta có: $\frac{1}{4}$=$\frac{1×3}{4×3}$=$\frac{3}{12}$ và $\frac{5}{3}$=$\frac{5×4}{3×4}$=$\frac{20}{12}$

Vậy quy đồng mẫu số hai phân số $\frac{1}{4}$ và $\frac{5}{3}$ ta được $\frac{3}{12}$ và $\frac{3}{5}$ .và $\frac{4}{7}$

Vì 5 x 7 = 35 nên ta chọn 35 làm mẫu số chung.

Ta có: $\frac{3}{5}$=$\frac{3×7}{5×7}$=$\frac{21}{35}$ và $\frac{4}{7}$=$\frac{4×5}{7×5}$= $\frac{20}{35}$

Vậy quy đồng mẫu số hai phân số  $\frac{3}{5}$ và $\frac{4}{7}$ ta được $\frac{21}{35}$ và $\frac{20}{35}$.

$\frac{3}{10}$ và $\frac{7}{9}$

Vì 10 x 9 = 90 nên ta chọn 90 làm mẫu số chung.

Ta có:  $\frac{3}{10}$=$\frac{3×9}{10×9}$=$\frac{27}{90}$ và $\frac{7}{9}$=$\frac{7×10}{9×10}$= $\frac{70}{90}$

Vậy quy đồng mẫu số hai phân số  $\frac{3}{10}$ và $\frac{7}{9}$ ta được $\frac{27}{90}$ và $\frac{70}{90}$

3. SGK Toán lớp 5 trang 14

3.1 Toán lớp 5 trang 14 Bài 6

Quy đồng mẫu số hai phân số:

Hướng dẫn giải:

+) $\frac{3}{4}$và $\frac{1}{6}$

Chọn 12 làm mẫu số chung.

Ta có:  $\frac{3}{4}$ =$\frac{3×3}{4×3}$= $\frac{9}{12}$và $\frac{1}{6}$=$\frac{1×2}{6×2}$

Vậy quy đồng mẫu số hai phân số  $\frac{3}{4}$và $\frac{1}{6}$ ta được $\frac{9}{12}$và $\frac{2}{12}$

+) $\frac{7}{10}$ và $\frac{5}{8}$

Chọn 40 làm mẫu số chung.

Ta có:  $\frac{7}{10}$ =$\frac{7×4}{10×4}$=$\frac{28}{40}$ và $\frac{5}{8}$ =$\frac{5×5}{8×5}$ =$\frac{25}{40}$

Vậy quy đồng mẫu số hai phân số  =$\frac{7}{10}$ và =$\frac{5}{8}$ ta được =$\frac{28}{40}$ và =$\frac{25}{40}$

+) $\frac{4}{9}$ và $\frac{5}{16}$Chọn 144 làm mẫu số chung.

Ta có:  $\frac{4}{9}$ =$\frac{4×16}{9×16}$=$\frac{64}{144}$ và $\frac{5}{16}$ =$\frac{5×9}{16×9}$ =$\frac{45}{144}$

Vậy quy đồng mẫu số hai phân số  $\frac{4}{9}$và $\frac{5}{16}$ ta được $\frac{64}{144}$và $\frac{45}{144}$

3.2 Toán lớp 5 trang 14 Bài 7

>, <,= ?

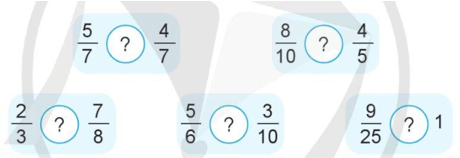
b) Sắp xếp các phân số $\frac{2}{3}$ ; $\frac{6}{7}$; $\frac{3}{4}$ theo thứ tự từ bé đến lớn.

Hướng dẫn giải:

a)

$\frac{5}{7}$ > $\frac{4}{7}$

$\frac{8}{10}$=$\frac{4}{5}$

$\frac{2}{3}$ < $\frac{7}{8}$

$\frac{5}{6}$ > $\frac{3}{10}$

$\frac{9}{25}$ < 1

b) Chọn mẫu số chung là 84.

Ta có $\frac{2}{3}$ =$\frac{2×28}{3×28}$= $\frac{56}{84}$

$\frac{6}{7}$ =$\frac{6×12}{7×12}$=$\frac{72}{84}$

$\frac{3}{4}$=$\frac{3×21}{4×21}$=$\frac{63}{84}$ Vì $\frac{56}{84}$  < $\frac{63}{84}$ < $\frac{72}{84}$ nên $\frac{2}{3}$ < $\frac{3}{4}$ < $\frac{6}{7}$.

Vậy các phân số đã cho viết theo thứ tự từ bé đến lớn là $\frac{2}{3}$ ;  $\frac{3}{4}$; $\frac{6}{7}$.

3.3 Toán lớp 5 trang 14 Bài 8

Dung và Đức cùng tham gia trò chơi leo dây với các dây có cùng chiều dài. Dung leo được $\frac{5}{8}$. sợi dây. Đức leo được $\frac{4}{10}$. sợi dây.

Theo em:

a) Dung đã leo được sợi dây màu nào? Đức đã leo được sợi dây màu nào?

b) Ai đã leo được đoạn dây dài hơn?

Hướng dẫn giải:

a) Dung đã leo được sợi dây màu cam, Đức đã leo được sợi dây màu xanh dương.

b) Chọn 40 là mẫu số chung. Ta có:

$\frac{5}{8}$=$\frac{5×5}{8×5}$=$\frac{25}{40}$; $\frac{4}{10}$=$\frac{4×4}{10×4}$=$\frac{16}{40}$

Vì $\frac{25}{40}$>$\frac{16}{40}$ nên $\frac{5}{8}$ > $\frac{4}{10}$